Golden Ratio is the answer to life: Part 2

The Golden Ratio – 1.618 – is also called the Divine Proportion. In Part 1 (Click here: Golden Ratio is the answer to life), we saw what Golden Ratio is, and how it is seen everywhere in the universe. We came to the conclusion that somehow the universe is very precise in many aspects. But how? Today we will see how this precision shows up in the universe, followed by a discussion on how the universe achieves this precision.

How is this Golden Ratio achieved in nature and the universe?

The next question that comes to our mind is how is our universe so precise in arranging everything with the exact number 1.618. The answer is Fibonacci Numbers. Just like I explained before, the Golden Ratio spirals will be formed by moving 1 unit, then 1 unit again, then 2 units, then 3, followed by 5, and so on. This is nothing but the series of numbers having a relationship with the previous number to produce the next number in the series. Start with 0 and 1. The next number is 0+1=1. After that comes, 1+1=2. Likewise, 1+2=3. Then, 2+3=5, and so on.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 etc.
(The next number is found by adding up the two numbers before it.)

As the numbers become bigger, they come closer and closer to the Golden Ratio.

A	B	Ratio
8	5	1.6
13	8	1.625
21	13	1.61538
…	…	…
233	144	1.618055
377	233	1.618025

Even our own Milky Way galaxy grows out in spirals and follows the Fibonacci Numbers, resulting in the Golden Ratio. Not just these particular numbers. You can take any random two numbers and make a series in this manner. As the numbers become bigger and bigger, we will approach the Golden Ratio. This is what makes the concept of Fibonacci so favorable in the universe. Let me take 190 and 2 and make a table like the above.

A	B	Ratio
190	2	95
192	190	1.0105
382	192	1.9895
…	…	…
6502	4016	1.619023
10518	6502	1.617656
17020	10518	1.618178

You can do this on your own as well. Take any two random numbers and add them. Take the sum and add it to the larger of the previous numbers. Generate a whole series of numbers like this, and divide two consecutive numbers. If you take the larger numbers, you will keep getting closer to the Golden Ratio.

Do we already know the significance of the Golden Ratio?

The concept of the Fibonacci numbers and the Golden Ratio was not unknown to our ancestors. Rishi Pingala came up with the concept of Matrameru, which is the same as the modern-day concept of the Fibonacci series converging to the Golden Ratio, but came hundreds and thousands of years before Fibonacci. He came up with the Matrameru while drawing possible combinations of syllables for writing shlokas. In Sanskrit, there are two kinds of syllables – Long (Guru) and Short (Laghu). I will call them 1 (Long) and 0 (Short) for simplicity. Long syllables require two beats and short ones require one beat. I will make a table with the possible syllable combinations for every beat.

Beats	Syllable combinations	Total number of combinations
1	0	1
2	00, 1	2
3	000, 01, 10	3
4	0000, 001, 010, 100, 11	5
5	00000, 0001, 0010, 0100, 1000, 011, 101, 110	8
6	000000, 00001, 00010, 00100, 01000, 10000, 0011, 0101, 0110, 1010, 1100, 1001, 111	13

Do you recognize the pattern in the total number of combinations? Yes! We generated the series we know today as the Fibonacci Series converging towards the Golden Ratio. So, knowledge always existed. He then formulated the Matrameru pyramid, which we know today as Pascal’s triangle.

There are some articles on the internet that state that just because the series was known, we cannot assume that the Golden Ratio was known. They say that it is a mere coincidence that the Fibonacci series was known but it was never used to relate to the concept of the Golden Ratio. However, it is important to remember the existence of the following Vedangas (Veda + Anga), or limbs of Vedic study that make use of the Golden Ratio:

• Chandas Shastra: This is exactly what was said in the table above about the two types of syllables. While it is clear that the combinations of meters that can be used in a shloka depend on the series, at much higher or complex systems, it can get a little tedious to track the combinations. Without knowledge of the correct ratio, it would never have been possible to generate the right meters for each shloka. And I don’t think I have to emphasize how extensive all Vedas, Puranas, and Upanishads are in volume.
  This is the exact problem faced with some corrupt completions of shlokas. Just using a meter being used through the verse to complete a shloka doesn’t make it correct. Careful consideration of the right combination is important, which was known earlier, and hence we have our books.
  It is easy to agree with me because you have confidence in our ancestors. But more important is to know why they are right so that you are able to explain when challenged. To clarify this point, I will take an example.
  Consider a verse from one of the Sanskrit Maha Kavyas, “Shishupala Vadha” by Magha. There are several great pieces of art in the whole work. The 27th stanza can be called one of the most exquisite palindromes ever written. The whole stanza is a palindrome and is called “Sarvatobhadra” or perfect in all directions.
  

In the front direction, we would read it as:

In the reverse direction, we would read it as:

This work is basically a sub-plot in the Mahabharata talking about the slaying of the evil Shishupala. This stanza in particular talks about the evil army enjoying the war and the cries of its opponents. For such exquisite poetry to have words, aesthetics as well as precision, some mathematical planning was necessary before writing.

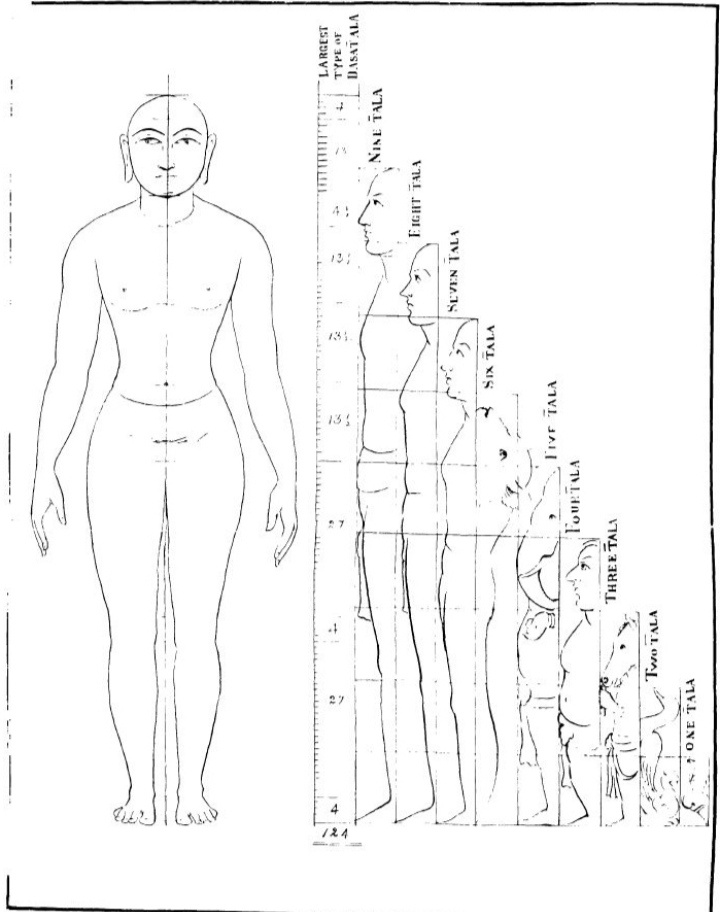
• Shilpa Shastra: This is an umbrella term consisting of all literature related to art, building, architecture, construction, patterns, and designs. Even Vaastu Shastra is included in this. In today’s time, we have measurement systems using kilometers, meters, miles, yards, etc. These are absolute scales and can be used independently. But according to measurement scales in Shilpa Shastra, the measurements were not done on an absolute scale, but rather on a relative scale using proportions called “Talamana Paddathi” (measurement using the Tala or palm of the hand). There were different types of width to length ratios like Samatata, Padadhika, Ardhadhika, and Padona. Ardhadhika ratios could be 1:1.5, 1:2.5, and so on. Even the ratios between 1:1.5 and 1:1.75 are considered to be part of Ardhadhika ratios. Hence, the Golden Ratio being 1:1.618 falls within this category. The Golden Ratio itself was called “Kanakumari”. The application of this ratio can be particularly found in the construction of specific types of idols for temples (Navatala Bimba and Dasatala Bimba). I will not go into the specifics of how the construction was done in order to keep it simple. In short, the Golden Ratio was always part of construction and designing, even if it was never pointed out especially. If anyone is interested in temple architecture and proportions, they can start reading by clicking here for a nice overview of the concepts.

But do we know the significance of the Golden Ratio to figuring out life?

Is the Golden Ratio the constant that defines life? Is it really true? Maybe, or may not be. It appears everywhere from quantum scales to galaxies. So, it seems unlikely that so many coincidences occur in the universe. But we must remember one thing. Nature does not know mathematics. Mathematics is just a man-made concept to explain things happening around us. So, the Golden Ratio is only a tool for understanding how the universe works. As seen throughout this series, the Golden Ratio is essential to the formation of several elements. So, the universe seems to be working on a set of rules, which shows us the precision of the universe. Our next focus is not studying the number. Our goal must be to understand the significance of this precision and study the reason for the precision of the universe and nature.

On a related note, we know that people from many cultures have collectively made profound contributions to science, mathematics, social science, and language over hundreds of centuries and decades. But shouldn’t the availability of knowledge be independent of culture? Point to ponder?

Get mystified! Get detoxified! Get Priya-fied!